[알고리즘] 정렬 -3
정렬
힙정렬
- 자료구조 ‘힙’의 장점을 활용한 정렬
-
임의의 값 삽입과 최댓값 삭제가 쉬움
- 힙
- 완전 이진 트리
- 각 노드의 값은 자신의 자식 노드의 값보다 크거나 같아야 함 (최대힙)
- 1차원 배열을 이용해서 구현
- 2n+1, 2n+2 방식으로 자식노드를 찾을 수 있음
- 완전 이진 트리
- 처리과정
- 1차원 배열을 힙으로 전환
- i = (n-1) to 1
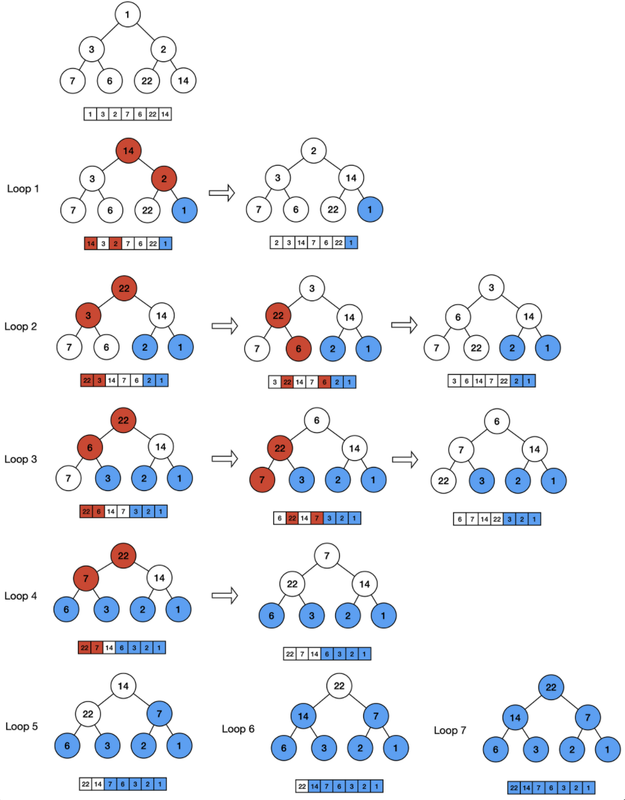
- 힙의 최댓값 삭제
- 힙의 재구성
- 다시 2부터 데이터 수만큼 반복
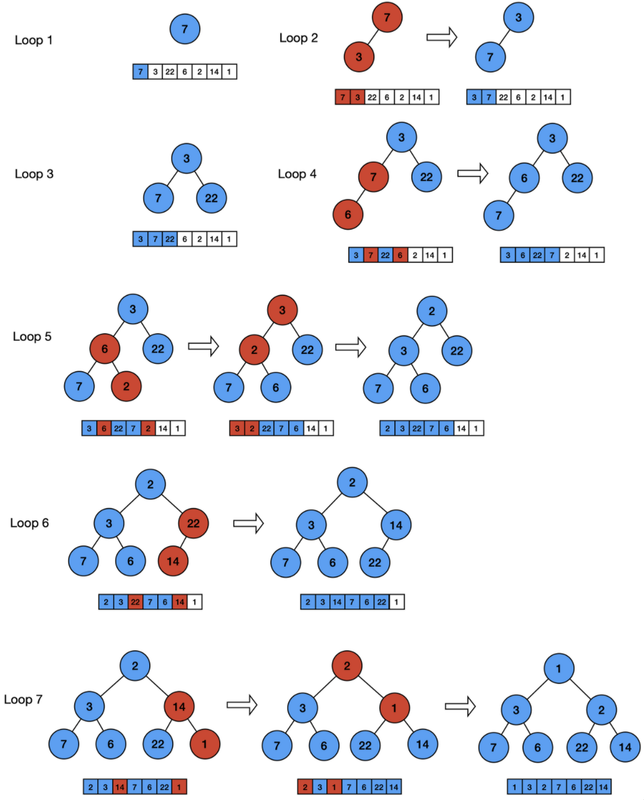
- 1차원 배열을 힙으로 전환
HeapSort(A[], n) {
// 단계1. 새노드의 삽입. 힙으로 구성
for(i=0; i<n; i++){
par = (i/2)-1;
while(par>=0 && A[par]<A[i]){
A[par]과 A[i]의 교환;
i = par;
par = (i-1)/2;
}
}
for(i=n-1; i>0; i--){
최댓값 A[0]와 마지막노드 A[i]의 교환;
cur=0; lch=1; rch=2;
// 힙의 재구성
do{
if(rch<i && A[lch]<A[rch]) lch=rch;
if(A[lch]>A[rch]){
A[cur]과 A[lch]의 교환;
cur = lch;
lch = cur*2+1;
rch = cur*2+2;
} else lch = i;
} while (lch<i)
}
}
- 초기 힙 구축
- 1차원 배열을 힙으로 변환하는 것
- 방법
- 주어진 입력 배열의 각 원소를 힙에 삽입하는 과정을 반복
- 주어진 입력 배열을 우선 완전 이진트리로 만든 후, 각 노드에 대해 아래에서 위로 + 오른쪽에서 왼쪽으로 진행하면서 해당 노드의 아랫부분이 힙의 조건을 만족할 수 있도록 트리를 따라 내려가면서 자신의 자손 노드들과의 위치 교환을 계속해 나가는 방법
- 주어진 입력 배열의 각 원소를 힙에 삽입하는 과정을 반복
- 1차원 배열을 힙으로 변환하는 것
-
재구성
- 특징
- 최선, 최악, 평균 수행시간 : O(nlogn)
- 초기 힙 생성 최댓값 삭제 및 힙 재구성
- 바깥 루프 : 입력 크기 n에 비례
- 안쪽 루프 : 완전 이진 트리 높이 logn에 비례
- 바깥 루프 : 입력 크기 n에 비례
- 최선, 최악, 평균 수행시간 : O(nlogn)
| 평균 성능 | 최선 성능 | 최악 성능 |
| O(nlogn) | O(nlogn) | O(nlogn) |
정렬 알고리즘
비교기반의 정렬 알고리즘
- 기본성능 O(n^2^) : 선택정렬, 버블 정렬, 삽입 정렬, 셸 정렬
- 향상된 평균 성능 O(nlogn) : 퀵 정렬, 합병 정렬, 힙 정렬
- 비교 기반 정렬 알고리즘 성능의 하한 = O(nlogn)
- 아무리 빨라도 O(nlogn)보다 효율적인 알고리즘은 구할 수 없음
이미 얻어진 데이터 분포 정보를 활용하는 정렬 알고리즘
- 계수정렬, 기수정렬, 버킷 정렬
- 선형시간 O(n)이 가능
계수정렬
- 주어진 데이터 중에서 자신보다 작거나 같은 값을 갖는 데이터의 개수를 계산하여 정렬할 위치를 찾아 정렬하는 방식
- 입력값이 어떤 작은 정수 범위 내에 있다는 것을 알고 있는 경우에 적용 가능
- k보다 작거나 같은 값을 갖는 데이터의 개수 => 정렬 순서상 k의 마지막 위치
- 자신보다 작거나 같은 값을 갖는 데이터의 개수의 효율적인 계산 방법
- 입력값의 범위 a~b에 해당하는 크기의 배열 COUNT[a..b]를 할당하고, 주어진 값들을 한 번 쭉 훑으면 각 입력값의 출현횟수의 누적값 계산이 가능
- 입력값의 범위 a~b에 해당하는 크기의 배열 COUNT[a..b]를 할당하고, 주어진 값들을 한 번 쭉 훑으면 각 입력값의 출현횟수의 누적값 계산이 가능
CountingSort(A[1..n], n) {
MIN = MAX = A[1];
// 입력값의 범위 MIN~MAX 계산
for(i=2; i<=n; i++){
if(A[i]<MIN) MIN=A[i];
if(A[i]>MAX) MAX=A[i];
}
for(j=MIN; j<=MAX; j++) COUNT[j]=0;
// 각 입력값의 출현횟수 계산
for(i=1; i<=n; i++) COUNT[A[i]]++;
//각 입력값의 출현횟수의 누적값 계산
for(j=MIN+1; j<=MAX; j++) COUNT[j]=COUNT[j]+COUNT[j-1];
//입력배열A[] -> 정렬배열B[]
for(i=n; i<0; i--) {
B[COUNT[A[i]]=A[i];
COUNT[A[i]]--;
}
return(B)
}
- 특징
- 입력값의 범위가 데이터의 개수보다 작거나 비례할 때 유용
- 입력값의 범위를 k라고 할 때 O(n+k) 시간
- k=O(n)이 되어야 선형 시간 O(n)에 동작
- 안정적인 정렬 알고리즘. 입력배열 A[]의 오른쪽의 것부터 뽑아서 배열 B[]의 오른쪽에서부터 저장
- 제자리 정렬 알고리즘이 아님. 입력배열에 따라 COUNT 추가 공간 필요
- 보편직이지 못한 정렬 알고리즘. 입력값의 범위를 미리 알아야함 + 추가적인 배열 필요
- 입력값의 범위가 데이터의 개수보다 작거나 비례할 때 유용
| 성능 | 안정적 알고리즘 | 제자리 정렬 알고리즘 |
| O(n) | O | X |
기수정렬
- 입력값을 자릿수별로 구분해서 부분적으로 비교하여 정렬하는 방식
- 주어진 데이터의 값을 자릿수별로 나누고 각 자릿수에 대해 계수 정렬과 같은 안정적인 정렬 알고리즘을 적용하여 정렬
- LSD 기수 정렬 : 낮은자리부터 높은자리로
- MSD 기수 정렬 : 높은자리부터 낮은자리로
RadixSort(A[], n){
// d 자릿수 LSD 기수 정렬
for(i=1; i<=d; i++){
각 데이터의 i자리의 값에 대해서 안적적인 정렬 알고리즘 적용;
}
return(A);
}
- 특징
- 계수정렬 사용 => O(n)
- 입력 데이터의 자릿수가 상수일 때 유용
- d 자리수 n개의 숫자들에 대해 계수 정렬을 적용하면 O(dn). 여기서 d를 입력 크기 n가 무관한 상수로 간주하면 O(n)
- 안정적인 정렬 알고리즘. 각 자릿수별로 정렬 알고리즘을 적용하므로 기수 정렬도 안정적
- 제자리 정렬 알고리즘이 아님. 전체 데이터 개수와 진법 크기만큼 추가 공간이 필요
- 계수정렬 사용 => O(n)
| 성능 | 안정적 알고리즘 | 제자리 정렬 알고리즘 |
| O(n) | O | X |
버킷정렬
- 주어진 데이터들의 값의 범위를 균등하게 나누어 여러개의 버킷을 만든 뒤
- 각 데이터를 해당하는 버킷에 넣고
- 각 버킷을 삽입 정렬과 같은 안정적인 정렬을 수행한 후
- 버킷 순서대로 각 데이터를 나열하는 정렬 방식
- 입력값의 범위 내에서 값이 확률적으로 균등하게 분포될 때 선형 시간에 동작
BucketSort(A[], n){
MIN = MAX = A[0];
// 입력값의 범위 MIN~MAX 계산
for(i=1; i<n; i++){
if(A[i]<MIN) MIN=A[i];
if(A[i]>MAX) MAX=A[i];
}
//버킷 구간의 크기 계산
INTERVAL = (MAX-MIN+1)/n;
// 각 데이터를 해당 버킷에 넣기
for(i=0; i<n; i++) A[i]를 Bucket[(A[i]-MIN)/INTERVAL]에 삽입;
for(i=0; i<n; i++) 삽입 정렬에 의해 Bucket[i]를 정렬;
Bucket[0], Bucket[1], ... 의 순서대로 데이터를 배열 B[]에 삽입;
return(B);
}
- 특징
- 입력 데이터의 값이 확률적으로 균등하게 분포할 때 유용
- 버킷의 개수가 입력 데이터의 개수에 비례해야 유용
- 위의 두조건이 성립할때 O(n)
- 안정적인 정렬 알고리즘. 데이터를 버킷에 넣을 때 그리고 각 버킷의 정렬 과정에서 상대적인 순서를 유지
- 제자리 정렬 알고리즘이 아님. 추가적인 저장공간 버킷배열의 크기와 배열B[]가 필요
- 입력 데이터의 값이 확률적으로 균등하게 분포할 때 유용