이진탐색 트리
- 이진트리
- 한 노드의 왼쪽 서브트리에 있는 모든 키 값은 그 노드의 키값보다 작다
- 한 노드의 오른쪽 서브트리에 있는 모든 키 값은 그 노드의 키값보다 크다
탐색 연산
- 루트 노드에서부터 시작해서 값의 크기 관계에 따라 트리의 경로를 따라 내려가면서 탐색 진행
삽입 연산
- 삽입할 원소를 탐색한 후, 탐색이 실패하면 해당 위치에 자식 노드로서 새 노드를 추가
삭제 연산
- 자식노드가 없는 경우(리프 노드의 경우)
- 자식 노드가 하나인 경우
- 자식 노드를 삭제되는 노드의 위치로 올리면서 서브트리 전체도 따로 올림
- 자식 노드가 2개인 경우
- 삭제되는 노드의 후속자 노드를 삭제되는 노드의 위치로 올리고
- 후속자 노드를 삭제되는 노드로 취급하여 자식 노드의 개수에 따라 다시 처리
성능 및 특징
- 키값을 비교하는 횟수에 비례. 이진 트리의 높이가 h라면 O(h)
- 모든 노드의 차수가 2인 경우 : O(logn)
- 모든 노드(리프노드 제외)의 차수가 1인 경우 : O(n)
- 삽입/삭제 연산 시 기존 노드의 이동이 거의 발생하지 않음
- 삽입 연산 : 노드의 이동이 없음
- 삭제 연산 : 상수 번 이동 (0,1,1 또는 2)
- 원소의 삽입/삭제에 따라 경사 트리 형태가 될 수 있음
- 최악의 수행시간 O(n)을 가짐
- 경사 트리가 만들어지지 않도록 트리의 균형을 유지해서 O(logn)을 보장
- 균형 탐색 트리(=탐색 트리의 좌우 서브트리가 같은 높이를 유지하는 자료구조) ex) 2-3-4 트리, 레드-블랙 트리, B-트리
2-3-4 트리
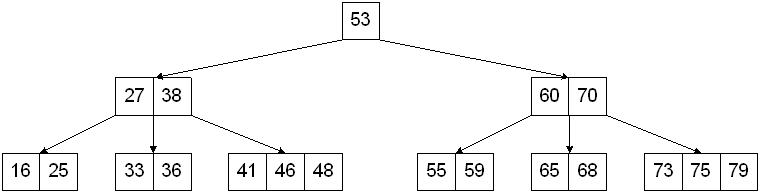
- 2-노드 : 1개의 키와 2개의 자식을 갖는 노드
- 3-노드 : 3개의 키와 3개의 자식을 갖는 노드
- 4-노드 : 3개의 키와 4개의 자식을 갖는 노드
- 각 노드의 한 키의 왼쪽 서브트리에 있는 모든 키값은 그 키값보다 작다
- 각 노드의 한 키의 오른쪽 서브트리에 있는 모든 키값은 그 키값보다 크다
- 모든 리프 노드의 레벨은 동일
삽입 연산
- 탐색 과정에서 4-노드를 만나면 항상 노드 분할을 우선 수행
- 노드 분할
- 1개의 4-노드 -> 3개의 2-노드로 만들고 중앙 노드를 부모노드로 만듬
성능 및 특징
- 탐색, 삽입, 삭제 연산의 시간 복잡도 - O(logn)
- 균형 탐색 트리 -> 트리의 최대 높이 logn
- 삽입/삭제가 일어나도 경사 트리가 되지 않음
- 루트 노드가 분할되는 경우에 한해서 모든 노드의 레벨이 동일하게 1씩 증가
- 2-3-4 트리를 그대로 구현하면 노드 구조가 복잡해서 이진 탐색 트리보다 더 느려질 가능성이 많음

