IM

작지만 단단하게

레드-블랙 트리

  • 이진 탐색 트리, 균형 탐색 트리

Red-black-tree-example-svg.png

성질

  1. 모든 노드는 검정이거나 빨강이다
  2. 루트 노드와 리프 노드는 검정이다
    • 모든 리프 노드는 NULL 노드이다
  3. 빨강 노드의 부모 노드는 항상 검정이다
    • 빨강 노드가 연달아 나타날 수 없음
  4. 임의의 노드로부터 리프 노드까지의 경로상에는 동일한 개수의 검정 노드가 존재한다
  5. 이진 탐색 트리의 성질
  6. 이진 탐색 트리의 성질

노드 구조

< 왼쪽 자식 노드 | 노드 색깔 | 키 값 | 오른쪽 자식 노드 | 부모 노드 | 형제 노드 >

빨강 노드가 연달아 나타나는 경우에 적용하는 규칙

  1. 부모 노드의 형제 노드가 빨강인 경우
    • 부모 노드, 부모 노드의 형제 노드, 부모 노드의 부모 노드 색깔을 모두 변경
  2. 부모 노드의 형제 노드가 검정이고, 현재 노드의 키 값이 부모 노드와 부모 노드의 부모 노드의 키 값의 사이인 경우
    • 현재 노드와 부모 노드를 회전 시킴
  3. 부모 노드의 형제 노드가 검정이고, 현재 노드의 키 값보다 부모 노드와 부모 노드의 부모 노드의 키 값이 큰(또는 작은) 경우
    • 부모 노드와 부모 노드의 부모 노드를 회전시키고 색깔을 변경

성능과 특징

  • 균형 탐색 트리
    • 어떤 두 리프 노드의 레벨 차이가 2배를 넘지 않는 균형 탐색 트리
    • 루트 노드에서 리프 노드의 경로상 ‘빨강 노드의 개수 < 검정 노드의 개수’
    • 루트 노드에서 리프 노드의 경로상에는 동일한 개수의 검정 노드가 존재
  • 탐색, 삽입, 삭제 연산의 시간 복잡도 : O(logn)
    • 최악의 경우 트리의 높이 O(logn)
  • 사실상 이진 탐색 트리
    • 탐색 연산은 이진 탐색 트리와 동일
    • 삽입 연산은 회전과 색깔 변경과 같은 추가 연산이 필요
  • 2-3-4 트리를 이진 탐색 트리로 표현한 것
    • 빨강 노드를 부모 노드와 묶어서 화나의 노드로 표현

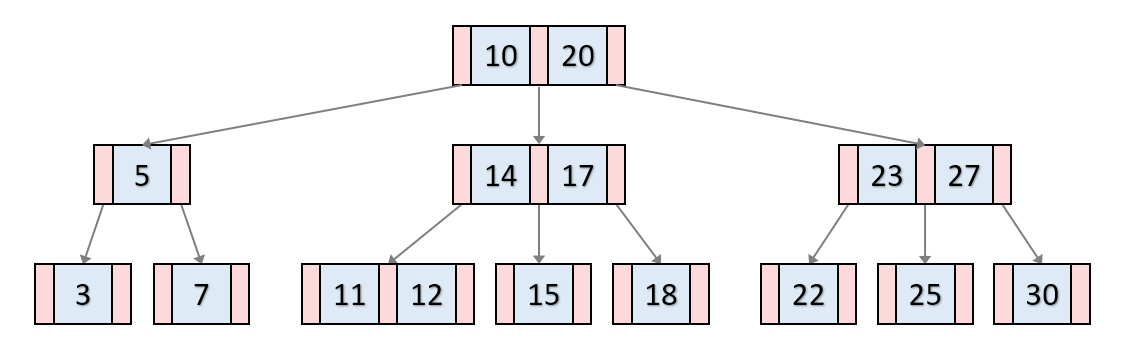
B-트리

  • 균형 탐색트리

성질

  1. 루트 노드는 1개 이상 2t개 미만의 오름차순으로 정렬된 키를 가짐
  2. 루트 노드가 아닌 모든 노드는 t-1개 이상 2t개 미만의 오름차순으로 정렬된 키를 가짐
  3. 내부 노드는 자신이 가진 키의 개수보다 하나 더 많은 자식 노드를 가짐
  4. 각 노드의 한 키의 왼쪽 서브트리에 있는 모든 키 값은 그 키 값보다 작음
  5. 각 노드의 한 키의 오른쪽 서브트리에 있는 모든 키 값은 그 키 값보다 큼
  6. 모든 리프 노드의 레벨은 동일함

images-emplam27-post-ddbae2c9-da94-457d-bad8-77ff6791255b-B.png

삽입 연산

  • 루트 노드에서부터 탐색을 수행하여 리프 노드에도 존재하지 않으면 해당 노드에 추가

  • 노드 분할
    • 탐색 과정에서 (2t-1)개의 키를 갖는 노드를 만나면, 이 노드를 t-1개의 키를 갖는 2개의 노드와 1개의 키를 갖는 노드로 분할
    • 삽입으로 인해 노드의 키의 개수가 2t개가 되는 것을 방지

성능과 특징

  • 탐색, 삽입, 삭제 연산의 시간 복잡도 : O(logn)
  • 트리의 높이 h, 각 노드에서 키의 위치를 찾는 시간 O(t) -> O(th)

    • 각 노드 -> 키의 개수 : (t-1)~(2t-1)개
    • 자식 노드의 개수 : t~2t개
    • 모든 리프 노드의 레벨은 동일
    • 트리의 높이 h -> O(logtn) n:키의개수
    • 각 노드에서의 키 관리에 레드-블랙 트리를 이용하면 O(t) 시간 -> O(logt)

  • 내부 탐색과 외부 탐색에 모두 활용
    • 내부 탐색의 경우
      • t=2 또는 t=3 정도의 작은 값으로 지정
      • t=2 -> 2-3-4 트리
    • 외부 탐색의 경우
      • 디스크를 사용하는 경우라면 t를 충분히 크게 지정
      • 한 노드의 크기가 디스크의 한 블록에 저장되도록 함

Updated: