IM

작지만 단단하게

Two pointers, Sliding window

연속된 자연수의 합 (3-5)

  • 설명 : N입력으로 양의 정수 N이 입력되면 2개 이상의 연속된 자연수의 합으로 정수 N을 표현하는 방법의 가짓수를 출력하는 프로그램을 작성하세요. 만약 N=15이면 7+8=15, 4+5+6=15, 1+2+3+4+5=15 와 같이 총 3가지의 경우가 존재한다.

  • 입력 : 첫 번째 줄에 양의 정수 N(7<=N<1000)이 주어집니다.

  • 출력 : 첫 줄에 총 경우수를 출력합니다.

  • 작성답안 - 2point

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Main t = new Main();
        Scanner scan = new Scanner(System.in);
        int num = scan.nextInt();

        System.out.print(t.solution(num));
    }

    public int solution(int num){
        int result = 0;
        int[] arr = new int[num/2+2];
        for(int i=0; i<num/2+2; i++){
            arr[i] = i;
        }

        int lt=0, sum=0;
        for(int rt=1; rt<arr.length; rt++){
            sum += arr[rt];
            if(sum==num) result++;
            while(sum>num) {
                sum -= arr[lt++];
                if(sum==num) result++;
            }
        }
        return result;
    }
}
  • 특징
    1. 투포인트 방식으로 시작점과 끝점을 만들어 연속수를 더하는 방식을 그대로 차용해서 사용함
    2. 단, 연속값을 합산할때에 중간값보다 큰 값을 두번이상 더할 일은 없으므로 배열에는 ‘num/2+2’ 값을 넣어줌
    3. num/2+1 값을 사용하는것이 맞으나 배열 특성상 idx가 0부터 사용되고, 편의상 idx와 값을 일치하고싶어서 한칸 더 사용함

  • 작성 답안 (수학적 풀이)
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Main t = new Main();
        Scanner scan = new Scanner(System.in);
        int num = scan.nextInt();

        System.out.print(t.solution(num));
    }

    public int solution(int num){
        int result = 0;
        int[] arr = new int[num/2+2];
        for(int i=0; i<num/2+2; i++){
            arr[i] = i;
        }

        int div = 0;
        for(int i=1; i<arr.length; i++){
            div += i;
            if(div>num) break;
            if(i!=1 && (num-div)%i==0) result++;
        }
        return result;
    }
}
  • 풀이 답안
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Main t = new Main();
        Scanner scan = new Scanner(System.in);
        int num = scan.nextInt();

        System.out.print(t.solution(num));
    }

    public int solution(int num){
        int result = 0;
        int[] arr = new int[num/2+2];
        for(int i=0; i<num/2+2; i++){
            arr[i] = i;
        }

        int div = 1;
        num--;
        while(num>0){
            num -= ++div;
            if(num%div==0) result++;
        }

        return result;
    }
}
  • 특징
    1. 예를들어 연속되는 2개의 값으로 15를 만들수 있을 경우, 15-1-2=12를 미리 해놓은 후 12%2를 처리하면 나머지가 0이 됨. 3개로 만들수있라면 15-1-2-3=9, 9%3=0.
    2. 15-1-2-3-4=5, 5%4!=0 이기때문에 연속되는 4개의 값으로는 15를 만들수 없음
    3. 이 때 1개의 수(15)로 15를 만드는것은 연속되는 수의 합이 아니기 때문에 나의 경우 조건에 i!=1를 주가했고, 풀이답안에서는 num을 num– 처리해둠.

    4. 내 풀이에서는 i=1부터 계속해서 증가해가면서 (num-div)%i==0가 성립할때만 카운트를 시킴
    5. 풀이 답변에서는 num–에 div를 계속해서 감소시키면서 num%div==0 경우 카운트 시킴

최대 길이 연속부분수열 (3-6)

  • 설명 : 0과 1로 구성된 길이가 N인 수열이 주어집니다. 여러분은 이 수열에서 최대 k번을 0을 1로 변경할 수 있습니다. 여러분이 최대 k번의 변경을 통해 이 수열에서 1로만 구성된 최대 길이의 연속부분수열을 찾는 프로그램을 작성하세요. 만약 길이가 길이가 14인 다음과 같은 수열이 주어지고 k=2라면 1 1 0 0 1 1 0 1 1 0 1 1 0 1 여러분이 만들 수 있는 1이 연속된 연속부분수열은

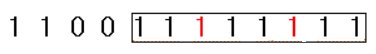
Image1.jpg

이며 그 길이는 8입니다.

  • 입력 : 첫 번째 줄에 수열의 길이인 자연수 N(5<=N<100,000)이 주어집니다. 두 번째 줄에 N길이의 0과 1로 구성된 수열이 주어집니다.

  • 출력 : 첫 줄에 최대 길이를 출력하세요.

  • 작성 답안

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Main t = new Main();
        Scanner scan = new Scanner(System.in);
        int num = scan.nextInt();
        int chk = scan.nextInt();
        int[] arr = new int[num];
        for(int i=0; i<num; i++){
            arr[i] = scan.nextInt();
        }

        System.out.print(t.solution(arr, chk));
    }

    public int solution(int[] arr, int chk){
        int result = 0, rt;
        for(int lt=0; lt<arr.length; lt++){
            rt = lt+1;
            int cnt=1, chg=0;
            while(rt<arr.length && (arr[rt]==1 || chg<chk)){
                if(arr[rt]==1) cnt++;
                else {
                    chg++;
                    cnt++;
                }
                rt++;
            }
            result = Math.max(result,cnt-1);
        }
        return result;
    }
}
  • 풀이 답안
import java.util.*;

public class Main {
    public static void main(String[] args) {
        Main t = new Main();
        Scanner scan = new Scanner(System.in);
        int num = scan.nextInt();
        int chk = scan.nextInt();
        int[] arr = new int[num];
        for(int i=0; i<num; i++){
            arr[i] = scan.nextInt();
        }

        System.out.print(t.solution(arr, chk));
    }

    public int solution(int[] arr, int chk){
        int result = 0, lt=0, cnt=0;
        for(int rt=0; rt<arr.length; rt++){
            if(arr[rt]==0) cnt++;
            while(cnt>chk){
                if(arr[lt++]==0) cnt--;
            }
            result = Math.max(rt-lt+1, result);
        }
        return result;
    }
}
  • 특징
    1. 나의 풀이는 매번 첫점이 이동할때마다 이후값을 다시 계산해야하는 낭비가 발생함
    2. lt, rt를 투포인트로 활용하고 cnt로 변경한 숫자를 집계하는 방법을 사용하는 것은 맞으나 루프를 도는 범위를 최대한 줄여야함
    3. 일단 길이는 매번 다시 카운트 하는것이 아니라 ‘rt-lt+1’을 길이라는 공식을 활용
    4. 시작점을 lt=0으로 정하고, for문을 이용해 rt만 한칸씩 증가
    5. arr[rt]가 0일때 변환 카운트 증가
    6. 그뒤 while문으로 변환카운트가 제한카운트수를 넘었을 경우 현재 시작점인 lt에서 가장 근접해있는 다음 0의 값을 찾아서 시작점을 변경하고 변환카운트 축소
    7. rt가 움직일때마다 rt-lt+1로 길이를 계산하고 이미 담겨있는 result와 비교해 최대값으로 반영

Updated: