IM

작지만 단단하게

Greedy기출문제 풀이

원더랜드(최소스패닝트리)

  • 설명 : 원더랜드에 문제가 생겼다. 원더랜드의 각 도로를 유지보수하는 재정이 바닥난 것이다. 원더랜드는 모든 도시를 서로 연결하면서 최소의 유지비용이 들도록 도로를 선택하고 나머지 도로는 폐쇄하려고 한다. 아래의 그림은 그 한 예를 설명하는 그림이다.

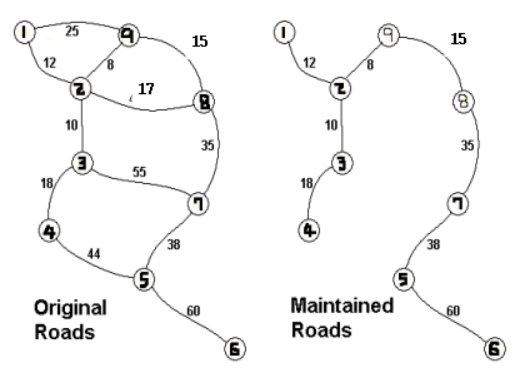
Image1.jpg

위의 지도는 각 도시가 1부터 9로 표현되었고, 지도의 오른쪽은 최소비용 196으로 모든 도시를 연결하는 방법을 찾아낸 것이다.

  • 입력 : 첫째 줄에 도시의 개수 V(1≤V≤100)와 도로의 개수 E(1≤E≤1,000)가 주어진다. 다음 E개의 줄에는 각 도로에 대한 정보를 나타내는 세 정수 A, B, C가 주어진다. 이는 A번 도시와 B번 도시가 유지비용이 C인 도로로 연결되어 있다는 의미이다.

  • 출력 : 모든 도시를 연결하면서 드는 최소비용을 출력한다.

  • 풀이 답안

import java.util.*;
import java.util.List;

class Edge implements Comparable<Edge> {
    int p1;
    int p2;
    int value;

    public Edge(int p1, int p2, int value) {
        this.p1 = p1;
        this.p2 = p2;
        this.value = value;
    }

    @Override
    public int compareTo(Edge o) {
        return this.value-o.value;
    }
}
public class Main {

    static int[] arr;
    static List<Edge> list = new ArrayList<>();

    static int answer=0;

    static void Union(int a, int b, int v) {
        int ra = Merge(a);
        int rb = Merge(b);
        if(ra!=rb) {
            arr[ra] = rb;
            answer+=v;
        }
    }

    static int Merge(int p){
        if(p==arr[p]) return arr[p];
        else return arr[p] = Merge(arr[p]);
    }

    public static void main(String[] args) {

        Main main = new Main();
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        arr = new int[n+1];
        for(int i=1; i<=n; i++){
            arr[i] = i;
        }
        int m = scan.nextInt();
        for(int i=0; i<m; i++){
            int a = scan.nextInt();
            int b = scan.nextInt();
            int c = scan.nextInt();
            list.add(new Edge(a, b, c));
        }
        Collections.sort(list);
        for (Edge edge : list) {
            Union(edge.p1, edge.p2, edge.value);
        }
        System.out.println(answer);
    }
}
  • 정리
    • union 방법을 기초로 하되 최소스패닝트리의 경우 이미 만들어진 노선은 다시 합칠 필요가 없고, 가장 최소값만 합치면 되기에 이에 우선값을 주면 됨
    • 따라 edge를 만들어 줄때 value순으로 정렬하고 이 배열을 기반으로 반복을 돌아
    • 작은 수로 이미 병합이 된 두 정점은 지나가도록 함

Updated: